Are computers ready to solve this notoriously unwieldy math problem?
The computer scientist Marijn Heule is always on the lookout for a good mathematical challenge. An associate professor at Carnegie Mellon University, Heule has an impressive reputation for solving intractable math problems with computational tools. His 2016 result with the “Boolean Pythagorean triples problem” was an enormous headline-grabbing proof: “Two hundred terabyte maths proof is largest ever.” Now he’s deploying an automated approach to attack the beguilingly simple Collatz conjecture.
First proposed (according to some accounts) in the 1930s by the German mathematician Lothar Collatz, this number theory problem provides a recipe, or algorithm, for generating a numerical sequence: Start with any positive integer. If the number is even, divide by two. If the number is odd, multiply by three and add one. And then do the same, again and again. The conjecture asserts that the sequence will always end up at 1 (and then continually cycle through 4, 2, 1).
The number 5, for instance, generates only six terms:
5, 16, 8, 4, 2, 1
The number 27 cycles through 111 terms, oscillating up and down—at its height reaching 9,232—before eventually landing at 1.
The number 40 generates another brief sequence:
40, 20, 10, 5, 16, 8, 4, 2, 1
To date, the conjecture has been checked by computer for all starting values up to nearly 300 billion billion and every number eventually reaches 1.
Most researchers believe the conjecture is true. It has enticed multitudes of mathematicians and non-mathematicians alike, but nobody has produced a proof. In the early 1980s, the Hungarian mathematician Paul Erdős declared: “Mathematics is not yet ready for such problems.”
“What we want to know is whether humans or computers are better at solving such problems.”
Marijn Heule
“And he’s probably right,” says Heule. For Heule, Collatz’s allure isn’t so much the prospect of a breakthrough as it is advancing automated reasoning techniques. After tinkering with it for five years, Heule and his collaborators, Scott Aaronson and Emre Yolcu, recently posted a paper on the arXiv preprint server. “Although we do not succeed in proving the Collatz conjecture,” they write, “we believe that the ideas here represent an interesting new approach.”
“It’s a noble failure,” says Aaronson, a computer scientist at the University of Texas at Austin. A failure because they didn’t prove the conjecture. Noble because they made progress in another sense: Heule views it as a starting point in determining whether humans or computers are better at proving such problems.
Translating math to computation
For many math problems, computers are hopeless, since they don’t have access to the vast oeuvre of mathematics amassed through history. But sometimes computers excel where humans are hopeless. Tell a computer what a solution looks like—give it a target and a well-defined search space—and then with brute force the computer might find it. Though it’s a matter of debate whether computational results amount to meaningful additions to the mathematical canon. The traditional view is that only human creativity and intuition, via concepts and ideas, extend the reach of mathematics, whereas advancements via computing are often dismissed as engineering.
In a sense, the computer and the Collatz conjecture are a perfect match. For one, as Jeremy Avigad, a logician and professor of philosophy at Carnegie Mellon notes, the notion of an iterative algorithm is at the foundation of computer science—and Collatz sequences are an example of an iterative algorithm, proceeding step-by-step according to a deterministic rule. Similarly, showing that a process terminates is a common problem in computer science. “Computer scientists generally want to know that their algorithms terminate, which is to say, that they always return an answer,” Avigad says. Heule and his collaborators are leveraging that technology in tackling the Collatz conjecture, which is really just a termination problem.
“The beauty of this automated method is that you can turn on the computer, and wait.”
Jeffrey Lagarias
Heule’s expertise is with a computational tool called a “SAT solver”—or a “satisfiability” solver, a computer program that determines whether there is a solution for a formula or problem given a set of constraints. Though crucially, in the case of a mathematical challenge, a SAT solver first needs the problem translated, or represented, in terms that the computer understands. And as Yolcu, a PhD student with Heule, puts it: “Representation matters, a lot.”
A longshot, but worth a try
When Heule first mentioned tackling Collatz with a SAT solver, Aaronson thought, “There is no way in hell this is going to work.” But he was easily convinced it was worth a try, since Heule saw subtle ways to transform this old problem that might make it pliable. He’d noticed that a community of computer scientists were using SAT solvers to successfully find termination proofs for an abstract representation of computation called a “rewrite system.” It was a longshot, but he suggested to Aaronson that transforming the Collatz conjecture into a rewrite system might make it possible to get a termination proof for Collatz (Aaronson had previously helped transform the Riemann hypothesis into a computational system, encoding it in a small Turing machine). That evening, Aaronson designed the system. “It was like a homework assignment, a fun exercise,” he says.
“In a very literal sense I was battling a Terminator—at least a termination theorem prover.”
Scott Aaronson
Aaronson’s system captured the Collatz problem with 11 rules. If the researchers could get a termination proof for this analogous system, applying those 11 rules in any order, that would prove the Collatz conjecture true.
Heule tried with state-of-the-art tools for proving the termination of rewrite systems, which didn’t work—it was disappointing if not so surprising. “These tools are optimized for problems that can be solved in a minute, while any approach to solve Collatz likely requires days if not years of computation,” says Heule. This provided motivation to hone their approach and implement their own tools to transform the rewrite problem into a SAT problem.
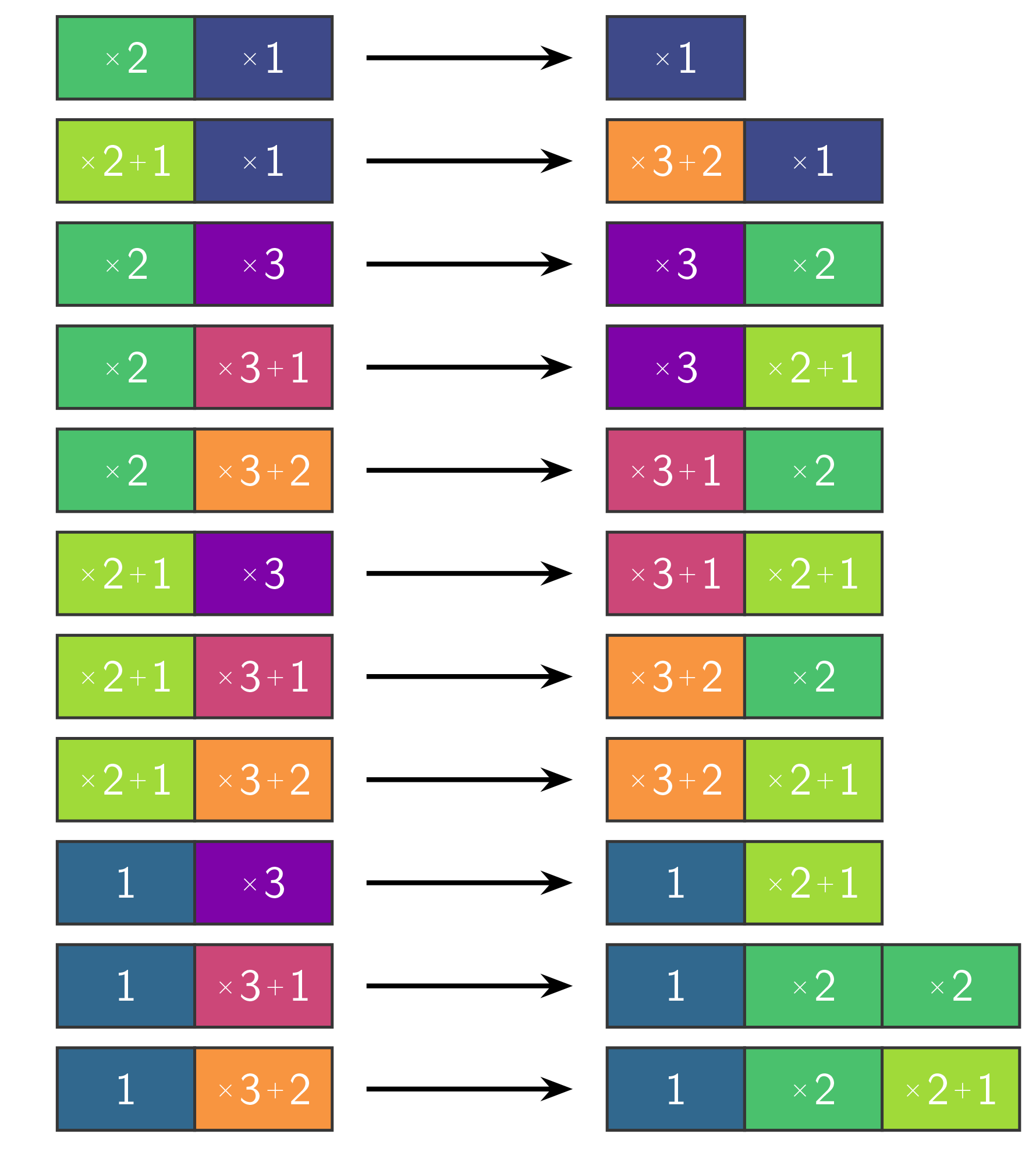
Aaronson figured it would be much easier to solve the system minus one of the 11 rules—leaving a “Collatz-like” system, a litmus test for the larger goal. He issued a human-versus-computer challenge: The first to solve all subsystems with 10 rules wins. Aaronson tried by hand. Heule tried by SAT solver: He encoded the system as a satisfiability problem—with yet another clever layer of representation, translating the system into the computer’s lingo of variables that can be either 0s and 1s—and then let his SAT solver run on the cores, searching for evidence of termination.
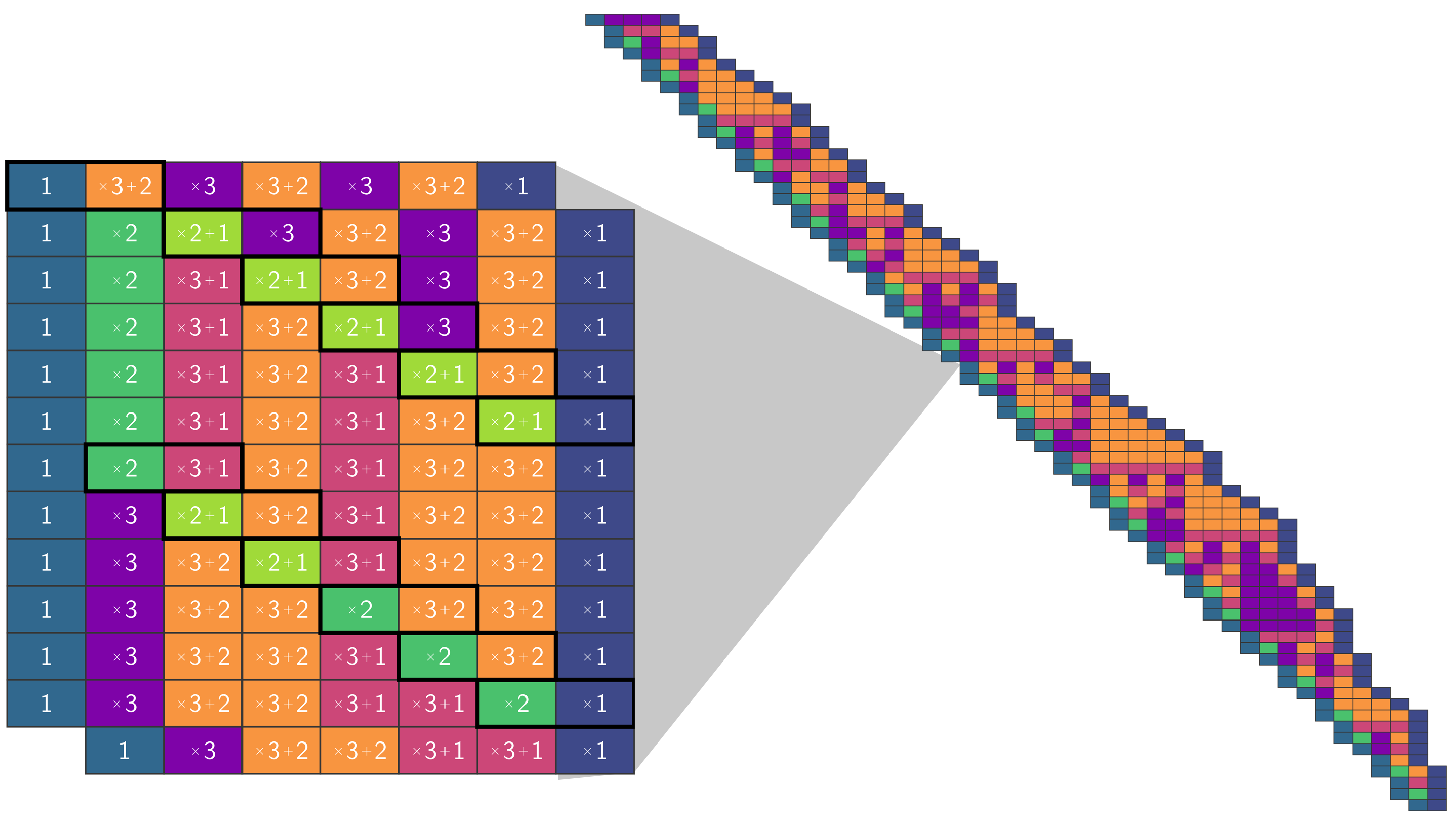
They both succeeded in proving that the system terminates with the various sets of 10 rules. Sometimes it was a trivial undertaking, for both the human and the program. Heule’s automated approach took at most 24 hours. Aaronson’s approach required significant intellectual effort, taking a few hours or even a day—one set of 10 rules he never managed to prove, though he firmly believes he could have, with more effort. “In a very literal sense I was battling a Terminator,” Aaronson says—“at least a termination theorem prover.”
Yolcu has since fine-tuned the SAT solver, calibrating the tool to better fit the nature of the Collatz problem. These tricks made all the difference—speeding up the termination proofs for the 10-rule subsystems and reducing runtimes to mere seconds.
“The main question that remains,” says Aaronson, “is, What about the full set of 11? You try running the system on the full set and it just runs forever, which maybe shouldn’t shock us, because that is the Collatz problem.”
As Heule sees it, most research in automated reasoning has a blind eye for problems that require lots of computation. But based on his previous breakthroughs he believes these problems can be solved. Others have transformed Collatz as a rewrite system, but it’s the strategy of wielding a fine-tuned SAT solver at scale with formidable compute power that might gain traction toward a proof.
So far, Heule has run the Collatz investigation using about 5,000 cores (the processing units powering computers; consumer computers have four or eight cores). As an Amazon Scholar, he has an open invitation from Amazon Web Services to access “practically unlimited” resources—as many as one million cores. But he’s reluctant to use significantly more.
“I want some indication that this is a realistic attempt,” he says. Otherwise, Heule feels he’d be wasting resources and trust. “I don’t need 100% confidence, but I really would like to have some evidence that there’s a reasonable chance that it’s going to succeed.”
Supercharging a transformation
“The beauty of this automated method is that you can turn on the computer, and wait,” says the mathematician Jeffrey Lagarias, of the University of Michigan. He’s toyed with Collatz for about fifty years and become keeper of the knowledge, compiling annotated bibliographies and editing a book on the subject, “The Ultimate Challenge.” For Lagarias, the automated approach brought to mind a 2013 paper by the Princeton mathematician John Horton Conway, who mused that the Collatz problem might be among an elusive class of problems that are true and “undecidable”—but at once not provably undecidable. As Conway noted: “… it might even be that the assertion that they are not provable is not itself provable, and so on.”
“If Conway is right,” Lagarias says, “there will be no proof, automated or not, and we will never know the answer.”
The human who’s arguably come closest is the mathematician Terence Tao, at the University of California, Los Angeles. In 2019 Tao proved the Collatz conjecture is “almost” true for “almost” all numbers (“almost” relies on two different technical definitions, nonetheless according with the plain English meaning).
Tao believes a human proof of the conjecture would be more mathematically meaningful—getting at the why of it— than a computer proof. “But having a major unsolved problem fall to an automated prover could supercharge a revolutionary transformation in how mathematicians use computer assistance in their work,” he says. “With a problem as intractable as this, we will take whatever insights we can get.”
What Heule and his collaborators are really after, however, is a scenario such that—using this approach, with this problem—the computer succeeds where the human fails, or vice versa. “At this point, we don’t know whether these techniques are much stronger than what humans can do by hand or not, or whether humans can do things that the computer can’t do,” Heule says. “What we want to know is whether humans or computers are better at solving such problems.”
To that end, let’s see who solves the Collatz conjecture first.

